TECHNIQUES DE SYNTESE D'IMAGE
INTRODUCTION
Parmi toutes les techniques utilisées en synthèse d'image, le couple modélisation par géométrie constructive (constructive solid geometry) et visualisation par la méthode de lancer de rayon (ray casting), est sans doute l'un des plus performant.Grâce à ces 2 techniques, il est en effet possible de combiner toutes sortes de solides entre eux, et de simuler des effets tel que les ombres portées, les reflets et les réfractions de façon simple et élégante.
Dans cette partie, nous étudierons tout d'abord rapidement les différentes méthodes de modélisation des solides et plus particulièrement la constructive solid geometry, puis nous étudierons le principe de l'algorithme de ray casting, nous étudierons enfin le problème de l'obtention d'image réalistes (calcul de l'éclairage, ombres, textures, etc).
METHODES DE MODELISATION DES SOLIDES
On peut globalement classer les différentes méthodes de modélisation de solides en 4 grands types [Bronsvoort 84] :
Modélisation par énumération spatiale
La plus répandu de ces représentations est la représentation par octree, dans laquelle un solide est représenté par subdivision hiérarchique de l'espace en éléments cubiques de taille décroissante et situés à l'intérieur du solide.
Modélisation par déplacement de contour
Un solide est représenté par un contour et une trajectoire le long de laquelle est déplacé ce contour, générant ainsi un volume. Les déplacements les plus couramment employés sont la translation et la rotation.
Modélisation par frontière (Boundary representation)
Un solide est représenté par l'ensemble des différentes surfaces qui le compose. Chaque surface elle même étant décomposée en ses différentes arêtes et sommets.
Modélisation par géométrie constructive (Constructive Solid Geometry)
Les solides sont modélisés par union (+), intersection (*), ou différence (-) de solides primitifs, ceux-ci pouvant être eux-mêmes générés par les différentes méthodes précédemment citées.Cette méthode est très générale et très efficace pour modéliser toutes sortes de solides, elle s'applique entre autres très bien à la modélisation de pièces mécaniques (applications de type C.A.O.).
En constructive solid geometry, un solide complexe est représenté de façon interne par un arbre binaire (arbre C.S.G.) dont les feuilles sont les solides primitifs et les n uds les différents opérateurs booléens (+, *, -) appliqués entre ces solides (voir figure 1).
La principale difficulté est alors d'appliquer les opérateurs booléens à l'ensemble des solides, ce qui conduit de façon générale à des calculs complexes dans l'espace.
Nous verrons que dans le cas du ray casting (et c'est pourquoi on les associe ensemble), ce calcul des opérations booléennes se ramène à un problème mono-dimentionnel, qu'il est alors très simple de résoudre.
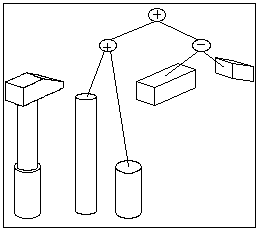
Figure 1. Un solide composé et sa représentation sous forme d'arbre C.S.G.
LA METHODE DE "RAY CASTING"
Analogie avec la photographie
Lorsque l'on prend une photographie, les rayons lumineux issus des diverses sources lumineuses, après avoir éclairé les divers objets de la scène, subissent diverses réflexions ou réfractions, atteignent l'objectif pour finalement impressionner le film.En fait, seul une infime partie des rayons émis atteindra finalement le film.
Le principe du "ray casting" est de simuler ce processus, mais en ne tenant compte que des rayons "utiles" (ceux atteignant finalement le film).
Pour cela, on parcourt à l'envers le trajet des rayons lumineux, depuis la pellicule (l'écran), jusqu'aux différentes sources lumineuses.
Principe de base
Pour chaque pixel de l'écran, un rayon partant de l' il, et passant par ce pixel, est lancé vers la scène (voir figure 2).On calcule alors les intersections de ce rayon avec tous les objets de la scène, la plus proche de celles-ci correspondant à un point de la surface visible.
A partir de ce point, et selon les propriété de l'objet (réfléchissant, transparent, etc), on lance alors récursivement divers rayons secondaires (rayons réfléchis, rayons transmis, rayons en direction des sources lumineuses, etc), pour déterminer quels objets ils traversent, l'ensemble de ces rayons formant un arbre.
L'intensité finale (la couleur) du pixel considéré est déterminée en calculant selon le modèle de réflexion choisi, la contribution de chaque noeud de l'arbre [Roth 80].
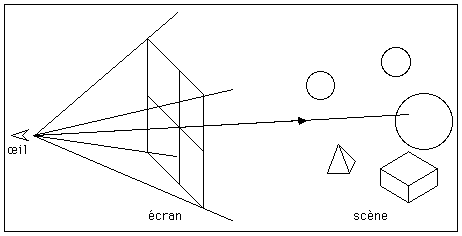
Figure 2. principe de la méthode de ray casting
Le calcul d'intersection
Le c ur de la méthode de ray casting est la procédure effectuant le calcul de l'intersection entre un rayon et les différents solides. Nous allons donc étudier celle-ci plus en détail.
Systèmes de coordonnées
Un système de coordonnées global
Un système de coordonnées écran
Un système de coordonnées local à chaque solide
Le repère global est le repère de référence absolu, et c'est le seul dont doit se soucier l'utilisateur. C'est dans celui-ci qu'il positionne et déplace les solides, la camera, les sources lumineuses.
Le système de coordonnées écran est utilisé comme repère de référence lors de la visualisation. C'est dans ce repère que seront émis les rayons partant de la caméra.
Chaque solide possède son propre système de coordonnées locales, et c'est dans ce repère qu'est exprimée l'équation du solide. C'est donc dans ce repère que sera calculée l'intersection avec un rayon.
Des matrices 4*4 (utilisation de coordonnées homogènes), permettront le passage d'un repère à un autre.
Paramètre d'entrée de la procédure :
Un rayon est simplement une droite dans l'espace. Il est défini par un point d'origine O de coordonnées (X0 Y0 Z0), et un vecteur directeur U de composantes (UX UY UZ).
On peut alors repérer la position d'un point M de coordonnées (X Y Z) appartenant au rayon par un unique paramètre l tel que :
X = l*UX + X0
X = l*UY + Y0
X = l*UZ + Z0
Paramètre de sortie de la procédure :
Cette liste est de la forme :
((l1 flag1 sol1) (l2 flag2 sol2) ... (ln flagn soln))
avec
l1, l2 ... ln : points d'intersection avec le rayon
flag1,flag2 ... flagn : drapeaux (1 quand on entre, 0 quand on sort)
sol1, sol2 ... soln : pointeurs vers les solide traversés
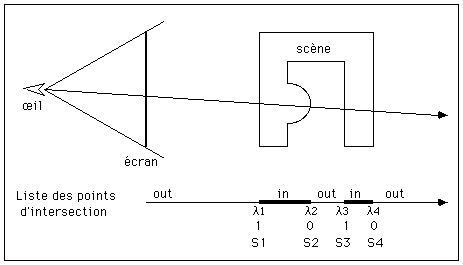
Figure 3 : un exemple d'intersection, et la liste de sortie correspondante
Intersection avec les solides primitifs
En effet un rayon entre et sort d'un solide par la surface de celui-ci, et cette surface n'est en fait que l'ensemble des surfaces des solides primitifs qui le composent.
Le calcul d'intersection a lieu dans le repère local du solide.
Il est donc nécessaire de tout d'abord transformer l'équation du rayon (son vecteur directeur et son origine) dans ce repère.
Il suffit alors de résoudre simultanément l'équation du rayon et celle du solide pour obtenir les éventuels points d'intersection.
Intersection avec un solide composé
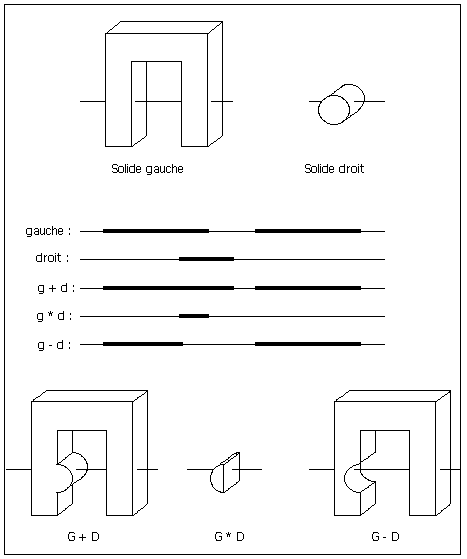
Figure 4 : exemples d'intersections en fonction des divers opérateurs
On peut décomposer cette combinaison en 3 étapes (voir figure 5) :
(1) Les listes des points d'intersection avec le solide gauche et le solide droit sont fusionnées, et ces points sont classés par ordre d'éloignement croissant.
(2) Chaque point est ensuite marqué comme point d'entrée ou de sortie suivant la classification des listes gauche et droite, et de l'opérateur booléen (voir table des lois de composition).
(3) Enfin, la liste obtenue est simplifiée pour éliminer les segments contigus de même nature.
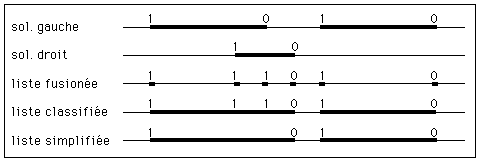
Figure 5 : exemple de combinaison de 2 listes (pour l'opérateur +)
----------------------------------------------------------
Opérateur Sol. gauche Sol. droit Sol. composé
----------------------------------------------------------
+ in in in
in out in
out in in
out out out
* in in in
in out out
out in out
out out out
- in in out
in out in
out in out
out out out
----------------------------------------------------------
Table des lois de composition
Remarque :
On peut noter que dans le cas des opérateurs * et -, s'il n'y a pas eu d'intersection à gauche, et quel que soit le résultat à droite, le résultat final est qu'il n'y a pas d'intersection.
Il est donc inutile dans de cas de calculer l'intersection à droite.
Efficacité et temps de calcul
L'algorithme présenté jusqu'à présent peut être qualifié d'algorithme minimal, est très simple, mais on peut facilement ce rendre compte qu'il est très coûteux en temps de calcul, même dans le cas le plus simple (pas de rayons secondaires).En effet, pour une image de résolution l *h pixels, d'un solide composé de n solides primitifs, et dont l'arbre C.S.G. est donc constitué de (n-1 ) sous arbres, le c ur de l'algorithme, c'est à dire la procédure de calcul d'intersection l *h *(2n-1 ) fois, dont l *h *(n-1) fois pour la procédure de classification, et l *h *n fois pour l'intersection avec les solides primitifs.
En prenant pour exemple une image 500*500, et un solide composé de 10 solides primitifs, on obtient les chiffres suivants :
4 750 000 appels de la procédure d'intersection
dont :
2 250 000 appels de la procédure de classification
2 500 000 appels de la procédure d'intersection avec les primitives
Le coût le plus élevé (en temps de calcul) revient à la procédure de calcul d'intersection avec les solides primitifs, car il faut à chaque fois transformer l'équation du rayon dans le repère local du solide (soit 18 multiplications et 15 additions de réels), et ensuite effectuer tous les calculs d'intersection eux mêmes.
Pour réduire le temps de calcul, il faut donc éviter d'appeler inutilement (rayon passant "à coté" du solide) la procédure de calcul d'intersection, et le faire le plus tôt possible dans le parcourt de l'arbre C.S.G.
Techniques de "boxing"
Pour cela, il faut trouver à la fois une enveloppe contenant au mieux le solide, et pour laquelle il est simple de calculer si un rayon passe à travers.
Il est aussi important de faire la distinction entre les rayons primaires (ceux partant de l'écran) dont on connaît au départ la direction, et les rayons secondaires (rayons réfléchis, diffractés, rayons vers les sources lumineuses) qui peuvent être eux de direction quelconque.
Rayons primaires
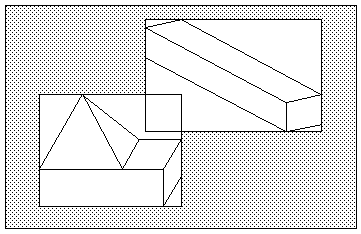
Figure 6 : exemple de solides et de rectangles enveloppes
Le test d'intersection du rayon passant par le pixel de coordonnée (X,Y) avec l'enveloppe se ramène alors à un simple test 2-D :
xmin X xmax
ymin Y ymax
Les coordonnées de ce rectangle seront stocké pour chaque solide (solide primitif et solide composé).
Il faudra bien entendu les recalculer à chaque fois que l'on modifiera les conditions de prise de vue.
Calcul de l'enveloppe pour un solide primitif :
On définira pour chaque solide un polyèdre contenant au mieux celui-ci. Ce polyèdre sera défini dans le repère local du solide par la liste de ses sommets.
On transformera ensuite les coordonnées de ces sommets du repère local, au repère de la caméra, puis on calculera la projection de ces points sur l'écran (en tenant compte de l'éventuelle perspective).
On prendra enfin comme dimension du rectangle les valeurs mini et maxi de ces projections.
Calcul de l'enveloppe pour un solide composé : (voir figure 7)
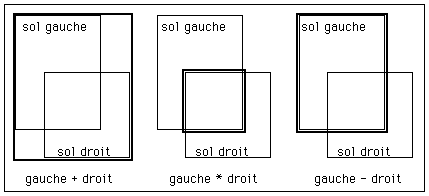
Figure 7 : règles de calcul de l'enveloppe d'un solide composé
Rayons secondaires
Le test d'intersection avec l'enveloppe se réduit alors au calcul de la distance entre une droite (le rayon), et un point (le centre de la sphère).
Si cette distance est supérieure au rayon de la sphère, il n'y a pas d'intersection (en fait il est plus économique de comparer le carré de ces 2 valeurs).
Méthode par raffinements successifs
Or on constate que des pixels voisins ont souvent la même (ou presque la même) intensité, surtout lorsqu'ils appartiennent à la même face d'un objet. C'est de cette constatation que découle l'idée de L'idée de base de la méthode de raffinements successifs [Bronsvoort84].
L'idée de base de cette technique est de commencer la calcul de l'image avec une résolution basse choisie par l'utilisateur. Pour cela, l'écran est divisé en carrés de coté égal à 2n pixels (par ex n = 3). Pour chaque carré, on calcule explicitement l'intensité du pixel correspondant au coin inférieur gauche du carré, et l'on attribue à tous les autres pixels du carré cette même intensité.
On obtient donc une image qui est une grossière approximation de l'image finale.
Le processus est ensuite répété en subdivisant chaque carré initial en 4 nouveaux carrés, mais on ne recalcule l'intensité de ceux-ci que si la différence entre l'intensité du carré initial et celle de ces voisins dépasse un certain seuil.
On concentre ainsi le calcul sur les zones de l'image présentant un fort gradient d'intensité, c'est à dire sur les bords et les arêtes des objets.
Le processus s'arrête à un niveau choisi à l'avance par l'utilisateur. Ce niveau peut être inférieur à la taille d'un pixel ce qui permet de faire de l'anti-aliasing sur l'image.
Cette méthode à pour inconvénient que de petits détails risquent de passer a travers les mailles du quadrillage, et donc d'être éliminés de l'image finale.
Elle est par contre très intéressante pour obtenir rapidement des images de basse résolution (pour faire des essais).
Diverses autres techniques plus complexes on été proposées :
Utilisation de volumes enveloppe différents suivant la forme des solides (utilisation de sphères, parallélépipèdes, et cylindres) [Weghorst84].
Pré-calcul en vue de repérer et marquer les surfaces visibles, pour pouvoir envoyer ensuite directement les rayons vers celles-ci [Weghorst84] .
OBTENTION D'IMAGES REALISTES
Jusqu'à présent, nous avons vu comment calculer l'intersection d'un rayon avec un solide. Il nous reste encore à voir comment calculer l'illumination de ce point d'intersection, et donc l'intensité du pixel correspondant.
Généralités sur l'éclairement des surfaces
L'énergie lumineuse incidente à une surface est transformée en 3 différentes composantes : Energie réfléchie par la surface, énergie transmise à travers la surface, et énergie absorbée par la surface.La distribution spatiale de ces 3 composantes est déterminée par les propriétés géométriques de la surface : forme, rugosité, présence de bosses, craquelures et autres irrégularités.
La distribution spectrale de ces 3 composantes est déterminée par les propriétés spectrales (la pigmentation) des différents matériaux constituant la surface. Elle est indépendante des propriétés géométriques de celle-ci.
C'est l'ensemble de ces propriétés qui déterminent finalement les caractéristiques de la lumière réfléchie [Carey 85].
Méthode de GOURAUD
Cette méthode basée sur la loi de Lambert est la plus simple, et permet de simuler des surfaces mates, diffusant parfaitement la lumière [Gouraud 71].
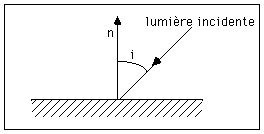
L'intensité lumineuse I réfléchie par la surface est donnée par la formule suivante :
I = k cos(i)
avec :
k : coefficient de réflexion
i : angle d'incidence
Méthode de PHONG
Cette méthode est plus sophistiquée et permet de tenir compte des réflexions spéculaires [Phong 75].
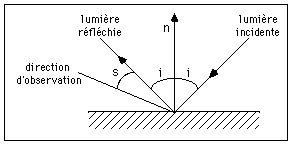
L'intensité lumineuse réfléchie I est donnée par la formule suivante :
I = Ia + kd cos(i) + ks (cos(s))n
avec :
Ia : intensité réfléchie due à la lumière ambiante
kd : coefficient de réflexion diffuse
ks : coefficient de réflexion spéculaire
i : angle d'incidence
s : angle entre la lumière réfléchie et la direction d'observation
n : coefficient tenant compte de la rugosité de la surface
Modèle plus complet
Ce modèle tient compte de la lumière réfléchie et de la lumière transmise. L'intensité lumineuse reçu par l'observateur est la somme d'une composante spéculaire, d'une composante transmise, et d'une composante due à la lumière diffusée par la surface [Witted 80].
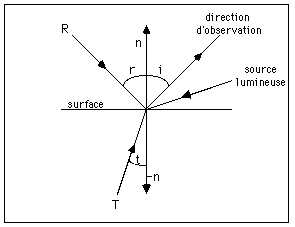
D'où la formule suivante :
I = Ia + kd D + kr R + kt T
avec :
Ia : intensité réfléchie due à la lumière ambiante
kd : coefficient de réflexion diffuse
D : intensité diffusée (obtenue par la méthode de Gouraud)
kr : coefficient de réflexion
R : intensité réfléchie (provenant de la direction R)
kt : coefficient de transmission
T : intensité transmise (provenant de la direction T)
Textures
La plupart des objets réels ne sont pas de couleur uniforme, soit parce que l'on a peint des motifs à leur surface, soit parce qu'il sont constitués de matériaux de couleurs différentes, soit même parce que ces matériaux sont hétérogènes (bois, marbre, etc).Il est donc important de pouvoir simuler ces différents types de textures.
Une première méthode consiste à modéliser une texture T par une fonction t(u,v), définie dans un espace de dimension 2 (généralement sur un carré de coté unité).
Pour chaque élément de surface du solide, on utilise alors une fonction de correspondance M (mapping function), entre tout point (de coordonnée x,y,z) de cette surface, et le carré unité [Carey 85].
(u,v) = M(x,y,z) d'ou T = t(M(x,y,z))
Il existe de nombreuses méthodes pour définir la fonction t représentant la texture. On utilise généralement une table ou est stockée la valeur de la texture en fonction des 2 paramètres u et v. Les valeurs de cette table peuvent être obtenues, soit en digitalisant une texture réelle, soit en utilisant une technique de synthèse de texture. Parmi celles-ci, nous pouvons citer : l'utilisation de grammaire (approche syntaxique), la synthèse par série de Fourier, et l'utilisation de fractales.
Cette méthode est bien adaptée à la représentation de surfaces qui ont été colorées (peintes), mais elle présente néanmoins un certain nombre de limitations dues principalement à la fonction de mapping M.
Il n'est en effet pas toujours simple de trouver une fonction permettant de passer de la surface du solide, à un plan, sans grande déformation, ou sans l'apparition de points singuliers, l'exemple type étant la sphère (problèmes de cartographie).
Il peut être d'autre part difficile d'assurer la continuité de la texture en plusieurs éléments de surface, et pour lesquels on à utilisé différentes fonctions de mapping.
Une autre méthode, appelée (solid texturing), permet de résoudre ces difficultés [Peachey 85].
On définit alors directement la texture T d'un point de coordonnées (x,y,z) de la surface du solide comme une fonction de texture t à 3 variables, celles-ci étant tout simplement les coordonnées du point considéré.
T = t(x,y,z)
Tout se passe alors comme si l'on avait sculpté le solide dans une matière définie par la fonction t. On n'a alors plus de problème de singularité ou de discontinuité dues au mapping.
Il est alors possible de représenter de façon réaliste des objets constitués par des matériaux hétérogènes, présentant des veines ou des inclusions, tels que le bois, le marbre, le granit, etc.
Tout comme pour la méthode précédente, on peut utiliser une table pour représenter la fonction t, ou bien obtenir directement la texture par synthèse.
Remarque :
Si les fonctions de texture sont le plus souvent utilisées pour connaître la couleur d'un point, il est également possible de les utiliser pour faire varier des paramètres tels que la réflectivité ou la transparence d'un solide (entre autres).
Modélisation d'irrégularités de surface
De nombreux objets réels ne sont pas absolument lisses, mais ils présentent au contraire de nombreuses irrégularités de surface (bosses, craquelures, nervures, etc), et il est donc important de pouvoir simuler de tels phénomènes.Il serait trop coûteux de modéliser séparément chaque irrégularité. On peut heureusement remarquer que de telles irrégularités, si elles n'apportent que de faibles distorsions à la forme de la surface, sont essentiellement perçues par leur effet sur la direction de la normale à cette surface, et donc sur la lumière réfléchie.
Pour simuler ces irrégularités, on utilise une fonction F(u,v) modélisant de petits déplacements dans le sens de la normale à la surface de référence [Blinn 77].
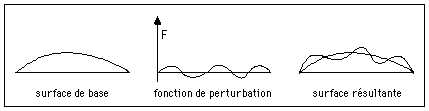
Connaissant F(u,v), on peut alors facilement en déduire pour chaque point les perturbations appliquées à la normale à cette surface.
La fonction de perturbation F peut être définie de la même façon qu'une fonction de texture, c'est à dire soit mathématiquement, soit à partir d'une table à 2 entrées (les paramètres u et v).
Modélisation des sources lumineuses
Un photographe de studio utilise de nombreux types de sources lumineuses pour mettre en valeur son sujet. Il utilise des spots pour éclairer des zones d'ombre, ou bien au contraire il utilise des diffuseurs pour atténuer des contrastes trop importants.Un bon système de synthèse d'image se devra donc de pouvoir modéliser ces différents types de sources lumineuses.
On pourra par exemple modéliser une lampe de type spot lumineux en la définissant comme une source ponctuelle possédant une direction d'éclairement privilégiée. L'intensité lumineuse sera maximale dans cette direction [Warn 83].
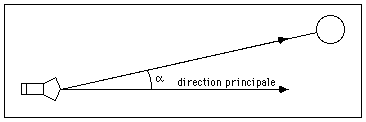
L'intensité I sera alors donnée par la formule suivante :
I = I0 cos(a)
avec
I0 : intensité maximale (dans la direction principale)
a : angle entre la direction d'éclairement et la direction principale
Utilisation de shade tree
Nous venons de voir que le calcul de l'éclairement d'un solide (le shading) peut être très simple (solide de couleur mate et uniforme), ou peut être au contraire très complexe et dépendre de nombreux paramètres. (solide semi-transparent taillé dans une matière hétérogène et présentant des irrégularités de surface).Il serait alors très lourd et peut efficace d'utiliser le même modèle pour ces 2 cas.
Une solution à ce problème est d'utiliser une structure plus souple permettant d'organiser un modèle en combinant entre eux des opérateurs élémentaires. On peut alors représenter ce modèle sous la forme d'un arbre (shade tree) [Cook 84].
Chaque opérateur sera un n ud de l'arbre, et les feuilles seront des paramètres tels que la direction de la lumière incidente, ou la normale à la surface.
La couleur finale sera obtenue en parcourant récurcivement l'arbre des feuilles jusqu'à la racine.
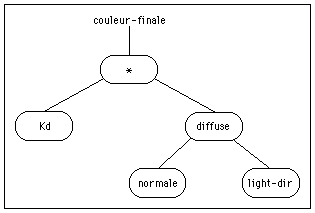
Exemple de shade tree pour le modèle de Gouraud
